During at least the
time period when water vapor (WV) and carbon dioxide (CO2) have been
accurately measured worldwide, 1988-now, and apparently for centuries, WV
increase has been responsible for the human contribution to Global Warming with
no significant net contribution from CO2 or any other greenhouse
gases.
The words ‘water
vapor’ can be a bit misleading. WV is a transparent gas. If something is
visible, like 'steam' or a cloud, it is not WV but is condensed liquid water
droplets or tiny bits of ice.
The term ‘vapor pressure’ has different meanings in different disciplines. In meteorology it means the partial pressure of WV in the atmosphere. In most other disciplines and general use, it means the pressure developed by the liquid as a result of its impetus to change phase and become a gas. This impetus depends only on the temperature of the liquid water. It is unambiguously called saturation vapor pressure. The pressure of WV in the atmosphere is identified as its partial pressure.
Another difference in term usage is the meaning of the word ‘feedback’. In engineering it usually refers to feedback factor, a dimensionless number which is the ratio minus 1 of response with feedback to the response if there were no feedback. In most science disciplines it refers to the magnitude of the response to a forcing which might or might not influence the cause of the forcing. In Climate Science it is measured in W/m2.
At a scale of
the size of atoms the atmosphere can be described as consisting of spinning and vibrating gas
molecules, with empty space between them, bouncing elastically off surfaces and
each other. Activity of all of the gas molecules determines properties which
can be measured such as temperature and pressure. Only certain gas molecules
significantly contribute to radiation heat transfer at planet temperatures. These are IR active in the
wavelength range of earth temperatures, are misleadingly called greenhouse
gasses (ghg) and include CO2 and WV. The radiation energy travels
from ghg molecule to ghg molecule (or between surface and ghg) at the speed of
light (in the atmosphere which is 99.97 % of the speed of light in a vacuum)
but the residual energy after thermalization effectively dwells in each CO2
molecule for up to about 1.1 second (from about 10 microseconds at sea level
pressure up to 1.1 second in isolation at top-of-atmosphere) making the
molecule warmer. The increased cumulative dwell time from increased WV
molecules is what causes the increased Greenhouse Effect (GHE). Dwell time is
AKA decay time.
Approximately 99% of dry atmospheric molecules are non-ghg; nearly all nitrogen and oxygen with about 1% argon. Near the surface, they are substantially warmed by thermalization of the earth-source thermal radiation energy absorbed by the ghg molecules and, at higher altitudes (starting a few meters or less above the surface), cooled by pressure decline and reverse-thermalization back to the ghg molecules. Above about 2 km altitude, because of steep decline with altitude of the population of WV molecules, lower pressure, and wider spacing between ghg molecules, outward directed radiation energy from WV molecules can make it all the way to space.
All molecule
species are fairly well mixed throughout the atmosphere with the exception of
WV. WV molecule population declines with altitude from average of about 8,000
ppmv (parts per million by volume) at sea level (in 1992) [34, 35] to, because of the low
temperature (~ -50 °C, saturation vapor pressure of ice 3.94 Pa [28] and total
pressure at 12 km of 19,400 Pa), to a maximum of about 3.94/19,400 = 0.000203 =
203 ppmv at the tropopause. The 8,000 ppmv (0.8%) average increases to about 4%
in the tropics.
The tropopause altitude averages about 12 km (39,370 ft) with up to 16 km or so at the equator. In addition to the population decline of WV molecules due to temperature decline, is the decline due to average pressure decline of 19.4/101.3 = 0.19 from a sea level pressure of 101.3 kPa. The combination results in an overall average WV molecule population decline up to the tropopause of about 8,000/203 * 101.3/19.4 = 206 to 1.
2. Thermalization
Thermalization
and/or reverse-thermalization (thermal conduction from surrounding molecules to
replenish energy radiated by a ghg molecule) occur continuously throughout the
atmosphere. Typical
TOA emission spectra are shown in Figure 1. A black-body emission curve (emissivity 1) for an average
global temperature of 288 K is a bit higher than a curve for the actual surface
which has an emissivity about 0.99. The TOA flux is the black trace in Fig 1. The
TOA and surface curves show radiation flux being slowed between the two
locations (absorbed/emitted by all ghg). On average, up to about 1.1 sec passes
between absorption and emission of a photon by a molecule (this is the decay
time which is about 1000 times longer than thermalization time). Prominently shown is the ‘notch’
associated with the CO2 absorb/emit band. The actual surface curve minus the TOA curve results in what is called
the Greenhouse Effect (GHE).
A much more extensive description of thermalization is at Section 4 of [19].
Hitran [2] using
Quantum Mechanics and measurements determines, besides many other things, the relative
absorb/emit intensity of water vapor molecules vs CO2 molecules.
Comparison at zero altitude, when scaled by atmospheric abundance, is shown in
Figure 2. At sea level, WV molecules (which have increased about 4.6 % since 1992) outnumber CO2 molecules in 2025 by about
8,400/420 ≈ 20 to one.
The relative increase of WV and CO2 over 30 years is
calculated as follows:
CO2
increase in 3 decades [3], 1988 to 2018: 407 - 348 = 59 ppmv.
Average global water vapor increase trend from Figure 5, which is a graph of NASA/RSS TPW data, is 0.0416/29 * 100 * 10 = 1.43 % per decade.
The ground level population of WV molecules in 1992 averaged about 8000 [34, 35]. Figure 3, at 30 degrees latitude (area to pole = area to equator) also averages global WV ≈ 8,000 ppmv. WV increase in 3 decades = 0.0143 * 8,000 * 3 = 343 ppmv.
Therefore, WV
increase has been 343/59 ≈ 5.8 times more than CO2 increase
1988-2018. (Much of the world human population has been falsely indoctrinated.
The false doctrine is that burning fossil fuels causes climate change.)
Above about 2 km and from below wavenumber 600, outward directed emission of WV can make it all the way to space. Some of the energy absorbed by CO2 molecules below the tropopause is redirected with respect to wavenumber via thermalization to WV molecules. Schwarzschild’s equation [40] accounts for this by assuming that “as radiation passes through an isothermal layer, its monochromatic intensity exponentially approaches that of blackbody radiation corresponding to the temperature of the layer.”
Well above the tropopause, radiation emitted from molecules there to space is primarily from CO2 molecules (partially indicated in Figure 1 by the spike at wavenumber 667). If you ignore the increase in water vapor (big mistake), near the surface, WV averages about 8,000 ppmv. WV above the tropopause is limited to about 203 ppmv because of the low temperature (~ -50 °C) while the CO2 fraction remains essentially constant with altitude at (in 2019) about 410 ppmv; up from about 295 ppmv in 1900. The increase in absorbers at ground level since 1900 is then about 8,410/8,295 ≈ 1%. The increase in emitters to space at high altitude (~> 20 km, 0.055 atm), and accounting for the lower atmospheric pressure, is (410 + 203)/(295 + 203) * 0.055 ≈ 0.068 = 6.8%. This (6.8%>1%) explains why CO2 increase does not cause significant warming (except near the poles). The result being that Climate Sensitivity (the temperature increase resulting from doubling the CO2 level) is not significantly different from zero.
More evidence that CO2 has no significant effect on climate is at Sect 2 of [19].
The exception at the poles is because it’s cold there at ground level so WV molecule count is already low. Therefore, transfer of energy to WV molecules which radiate it to space is negligible.
WV increase is a
cause of warming (average global temperature increasing) because it is a ghg.
Part of WV increase is a result of surface water warming because its saturation
vapor pressure increases with temperature. The saturation vapor pressure increase
causes an increase in the rate of WV molecules being forced into the atmosphere
(when the atmosphere at ground level is less than saturated with WV which is
nearly always the case). Additional sources of WV-increase include increased
human activity (3.1 billion more people on the planet in 2024 than 1988) and
irrigation causing increase in global average residence time, and decrease in condensing out
WV in cold ocean waters. This is discussed further in Section 7.
In the atmosphere, condensed water can exist as water, ice or super-cooled water [26] (super-cooled water is liquid water below 0.0 °C). Accurate numerical values for saturation vapor pressure of liquid water [27] and ice [28] are graphed in Figure 4. Saturation vapor pressure for super-cooled water can be calculated using the Bolton equation [25]. The Bolton equation for saturation vapor pressure in kPa vs temperature in C is
p = 0.6112 * e^(17.67 * T /
(T+243.5)) (1)
As shown in Figure 4, saturation vapor pressure increases progressively with temperature. Of interest is the % increase in saturation vapor pressure per degree increase in temperature. This is readily calculated from the numerical data for both liquid water and ice from:
1/1 increase/Tave = (pj
– p(j-1)/(Tj – T(j-1))/Tave (2)
Where,
1/1 = %/100
j and (j – 1)
are adjacent values in the table
Tave = average
temperature of the adjacent values.
The same thing
for super-cooled water is obtained using the first derivative of the Bolton
equation which is
dp/dT = p * 17.67 * 243.5/(T+243.5)^2 (3).
This, divided by p to get the 1/1 value curve, is shown in the bottom graph at Fig. 4.
Saturation vapor pressure depends ONLY on the temperature of the ice or liquid water. The 1/1 change in saturation vapor pressure per Celsius degree for water, ice and super-cooled water are shown in the lower graph of Figure 4.
As shown in Fig 4, the warming of cold (≈ 10 °C) water increases WV about
7%/C deg compared to warm (≈ 30 °C) water at about 5.7%/C
deg of temperature increase.
Figure 4: Saturation vapor pressure of ice &water and fractional rate of change per C degree change vs temperature.
The atmospheric temperature decreases with altitude so the accommodation for WV increases with altitude to about 12%/C° at the tropopause (°C is a temperature, C° is a temperature difference and is used interchangeably with K for Kelvin degree). Although the accommodation per degree increases with altitude, the magnitude of a temperature change usually decreases with altitude faster with the result that as absolute humidity increases, relative humidity usually slightly also increases.
Based on ocean temperatures from [29], the area-weighted change in saturation vapor pressure per C degree at sea level is about 0.0633 / C°. The amount of compounding is unknown but cannot be greater than 0.0633+0.0633^2+0.0633^3+… = 0.0676/C°. It is conservatively estimated to be about 0.067/C° = 6.7%/C°
The accelerated
increase in WV, above that determined from just global temperature increase, is
expected from the surge in irrigation and human population with accompanying increase in WV average residence time and has also been measured. Average
measured global atmospheric water vapor (total from surface to TOA) over the
years is provided here at Figure 5.
Figure 5: Average clear air Total Precipitable Water over all non-ice-covered oceans as measured by NASA/RSS using satellite based instrumentation and with extrapolation by me. (Left graph is by month, right graph is by year average.). Estimated near future minimum trend is 29.7 mm. Estimated near future maximum is the slope of the recent monthly trend.
Both WV and CO2
have increased since before both have been accurately measured worldwide.
The CO2 is well mixed and its increase is directly reported in ppmv [3].
Water vapor increase is measured and reported in kg/m^2 [5]. Average WV is
about 29 kg/m^2. The WV increase in ppmv is obtained from the TPW anomaly data by
first calculating the fraction of the atmosphere that is WV. The weight of the
atmosphere is 14.696 psi = 10332 kg/m^2 so the fraction by weight is 29/10332 =
0.002807. This times the ratio of molecular weights gives the average WV for
the entire atmosphere in ppmv. WV = 28.96/18.015 * 0.002807 = 0.004512 or 4512
ppmv. The values for ppmv WV are then the values by weight (plus an offset of
0.48 kg/m^2 to get the ppmv to start from zero) times 4512 ppmv/29 kg/m^2. This
is shown in Figure 5.1 along with the values for CO2. The ratio of
the slopes discloses that, in the total atmosphere, WV molecules have been increasing about 6.4739/2.0459
= 3.16 times faster than CO2 molecules.
The same calculation at ground level, because of the higher level of WV (about 8000 ppmv), results in WV increasing there about 5.6 times faster than CO2.
Figure 5.1: Comparison of WV increase in ppmv and CO2 increase in ppmv in
the total atmosphere.
6. World Sources of Increased
Water Vapor
Irrigation, industrialization, and, increasing population have
been contributing to the rise in atmospheric WV above that from feedback due to
liquid water temperature increase. A survey of available on-line literature
provides direct and indirect quantification of significant global sources of
the extra increase.
Worldwide about 86% of irrigated area is flood irrigated
[20]. To simplify calculation, assume all irrigation is flood irrigation
approximated as furrow type [16]. Optimum frequency is to flood the furrows
about every 10 days [17]. Thus about half the area is covered by water 10% of
the time where evaporation from the water is about one meter per year [18] and
the rest of the time, the additional evaporation is assumed to be according to
the calculated evapotranspiration. Evapotranspiration prior to irrigation must
have been low or irrigation would not be done. Evapotranspiration with
irrigation, to be cost effective, is most likely to be much more than
calculated. These two uncertainties are assumed to approximately cancel each
other. A further assumption is that, on average, irrigation is applied for
about 1/3 year. The total amount of WV resulting from irrigation is then
[(0.1 * (1 + 0.45)/2
+ 0.9 * 0.45) * 266E10]/3 = 42.3E10 m3 /y = 42.3E13 kg/y (k)
These calculations are summarized in Table 1
|
Water vapor source |
E13 kg/y |
% |
|
Irrigation |
42.3 |
90.0 % |
|
Transportation fuel |
0.4 |
0.8 % |
|
Fossil fuel for electricity generation |
0.3 |
0.7 % |
|
Cooling towers, etc. for electricity generation |
4.0 |
8.5% |
|
Total |
47.0 |
100 % |
Table 1: Summary of
contributions to atmospheric water vapor.
WV increase above that due to feedback from liquid water
temperature increase results about 90 % from irrigation. WV added by irrigation
is particularly influential because it is added at locations where natural WV
is low and because the liquid water is shallow, it is quickly and substantially
warmed by the sun.
Figure 6.1: Typical WV distribution over the planet. [39]
At about 35 degrees latitude from the equator the vapor
pressure in the oceans is about the same as the average partial pressure of WV
in the atmosphere. Beyond that, WV is sucked out of the atmosphere by cold
ocean water. Warming of this cold ocean water would reduce the rate of
absorption/condensation resulting in increase in WV.
The lower panel in Figure 4 shows that the fractional rate
of change of saturated vapor pressure is larger at lower temperature so the
reduction of absorption per degree change in temperature is greater than the
increase in evaporation in warm waters.
7. Comparison of measured WV with WV increase
calculated from feedback over a long time period.
The measured increase in WV with time, shown in the left
panel of Figure 5, results from increase in average residence time, increase in
precipitation, or some combination thereof. The slightly longer average residence time
results because of the time for the WV to travel from the low precipitation
area, where it is added, to the area where it precipitates. Increased WV
results from increasing population in deserts with mist generators, swamp
coolers, swimming pools, etc. and irrigation.
As described in Section 4, as the temperature of liquid surface water increases, its saturation vapor pressure increases which, if the atmosphere is not already saturated, forces more WV molecules into the atmosphere. This contributes to a net feedback from all factors which caused the temperature to increase. A conservative value for average global WV increase per degree C (actual WV increase from feedback will be less than so-calculated) was estimated in Sect 4 from available measured data to be 6.7% = 0.067 1/1. The large effective thermal capacitance of the planet is a main contributor to the conservatism. The temperature rise is in response to the time-integral of the forcing (IR absorption effect of WV) so, lacking other factors, it will lag the feedback forcing.
Except for UAH, reported temperatures by the several agencies are subject to uncertainties in estimated Heat Island Effect. UAH 6.1 [42] temperature data are used in the calculation of atmospheric WV
A graph of the UAH 6.1 temperature anomalies over the same period as covered by accurately measured average global WV is shown in Fig 7.
Figure 7: UAH
temperature anomalies from Jan 1988 thru Dec 2024 from numerical data reported at
[42].
The WV increase
rate that would result from just temperature increase rate can be calculated by
multiplying temperature regression increase rate * 0.067 * global average WV. Iteration
is required to converge on the average WV but converges very quickly. For WV
increase 1988 thru 2024 (37 yr) using UAH temperatures, this is:
0.016484 * 0.067 * 28.84 = 0.0318
mm/yr
The regression
slope for the measured WV is obtained from Fig 5. This calculation shows that
the measured WV is 0.0447/0.0318 = 1.406 times as much, or about 40 % more than
from just planet warming falsifying the assumption by many Climate Scientists
that WV increase is just feedback from temperature increase caused by CO2
increase. Uncertainties of 0.111 on the temperature increase of 0.61, 0.0005 on
the 0.067, 1 on the avg calculated WV of 28.8 and 1 on the measured WV of 29 results
in the probability that the hypothesis is falsified is about 99.38 %.
The ratio, measured-WV-increase/calculated-WV-increase-from-temperature-increase, was calculated for several previous years. The slopes for measured WV were obtained from the regression equation provided by EXCEL for each period of study. The slopes for WV due to temperature increase were obtained by calculating the temperature increase for each period of study, calculating the WV increase for each temperature increase and determining the slope of WV increase by dividing it by each period of study. The results are shown in Figure 7.1. This shows a most likely ratio of about 2.0 in 2016 (the 2016 calc was triple checked) for an even higher probability that measured WV increase does not result from just feedback. The decline after 2016 probably results from the measured increasing AGT trend combined with a roll-off in the rate of world population increase and improvement with leveling off and perhaps even decrease in needed irrigation due to increasing yield resulting from increasing CO2.
Figure 7.1: ‘extra’ WV over time period.
Sea Surface Temperatures (SST) can also be used to calculate WV increase. Sources were found that report from 1988 [43, 44]. SST reported from 1988 are shown in Fig 7.1.1 for two data sources. Offset does not matter because only the regression slope is used.
Figure 7.1.1: Sea
Surface Temperature anomalies.
Applying the above calculation method results in Figure 7.1.2 which shows, in 2000 and before, the measured WV more than twice the maximum possible from just SST warming rate for two additional sources of SST [45, 46]. This shows with even higher confidence that the Climate Science consensus that ‘WV increase results from average global temperature increase caused by CO2 increase’ is wrong.
Figure 7.1.2: In
2000 and before, measured WV was more than twice the maximum possible from just
SST increase.
A perhaps clearer display of the ‘extra’ WV is at Figure 7.1.3. This compares the measured WV increase rate with the maximum possible WV increase rate as a result of sea-surface-temperature increase, the Clausius-Clapeyron relation and a conservative nominal TPW level of 29 kg/m^2. The measured WV is the regression slope of the TPW measurements from 1988 for each year. The maximum possible is the regression slope from 1988 of the TPW values calculated from the sea-surface-temperature anomaly for each year. The TPW anomaly value for each year is the temperature anomaly * the TPW change per unit * average global TPW e.g. T * 0.067 * 29 kg/m^2. The results shown on the graph reveal the decade or so when measured WV substantially exceeded the maximum WV that could occur as a result of just SST warming.
Figure 7.1.3: Comparison
of regression slopes of measured WV increase and WV increase calculated from
temperature increase of the sea-surface-temperature.
Figure 7.1.4 is an example of determination of the measured and calculated TPW trends for 1988 to 2005. The TPW calculated from yearly average sea-surface temperatures reported by EPA are shown in blue and the monthly measured TPW values reported by NASA/RSS are shown in orange. The regression equations, calculated by EXCEL, are shown in boxes of the same colors. The first number in each box is the slope of the regression line which is the trend in kg/m^2 per year (or mm equivalent depth increase per year). This assessment was made for the period from 1988 to each year noted. The regression slopes (TPW trends) for each noted year are shown on Figure 7.1.3.
Figure 7.1.4: Measured
TPW and TPW calculated from SST reported by EPA.
The progress of the comparison over time can be obtained by numerical integration. The temperatures reported are the average for each month. The month-to-month temperature change (which drives WV change) is the difference between reported values. The average, (WV(n-1) +WV(n-2))/2, is used to minimize bias. The file for calculated change in WV due to average global temperature change is generated in EXCEL where each row contains:
WVn = calculated WV in month n, kg/m^2
Tn = reported temperature anomaly in month n, C°
Y = effective
rate of WV increase resulting from feedback of temperature increase, 0.067/C°
(= 6.7 %/C°)
F = value added to bring regression trend for WV calculation
for detrended temperature trajectory up to zero slope. When using UAH 6.1
(University of Alabama in Huntsville) temperatures, F = 0.000626. This corrects
for an artifact that arises as a result of interaction between data set and
integration algorithm.
Results using the above algorithm are shown in Fig 7.2 along with the measured WV. The difference in rates is the ratio of the slopes. That is, in Dec, 2024 the measured WV increase is about 1.4 times as high as significantly possible from just planet warming. Calculation is shown below graph (Fig 7.2). This assessment corroborates the value calculated previously for the same date falsifying the assumption by many Climate Scientists that water vapor increase is just feedback from temperature increase caused by CO2 increase.
Figure 7.2: Measured
WV and calculated WV based on UAH 6.1 average global temperatures [42]. (WV
increase 6.7%/K)
Alternatively, if there is no increase in average residence
time, the average global precipitation must increase by (29.75 – 28.25)/28.25 =
0.0531 1/1 or about 5.3 % in 37 years. Precipitation is about 1000 mm/yr so the
total increase would be 53/37 = 1.432 mm/yr. Part of the increase in WV results
from increase in temperature of the liquid water. The WV increase from the
temperature increase of the liquid water is 0.067 * 0.01648 * 28,25 = 0.031
mm/yr. The increase due to all human activity is then (1.432-0.031)/0.92 or
about 1.52 times as much precipitation increase as estimated in Sect 6. Anecdotal
comments are that annual rainfall is at an ‘all time high’. If true, this would
lessen the already tiny increase in average residence time
A corroboration of the long-term temperature trend is as follows: Assume that, at the beginning of the warm up, the temperature increase was caused by something else. Then the WV increase can be calculated from that temperature increase using the saturation vapor pressure vs temperature for water and the assumption that % increase in WV = % increase in saturation vapor pressure. But the WV has increased more than that so there has to be an additional cause of WV increase or a reduction of the condensation and/or absorption of WV by cold ocean water.
Figure 9: Scatter graph of WV vs HadCRUT5 measured
data.
This provides
fertile ground for those motivated to mislead to cherry-pick periods where the
increasing side of fluctuations drives both WV and outgoing-longwave-radiation
up.
11. Climate
change without CO2 change and CO2 change without otherwise
accounted for climate change.
A main concern from burning fossil fuels, especially coal, is the production of CO2 which many believe is a primary contributor to climate change. Proxy measurements covering the Phanerozoic eon (last 540 million years) show substantial changes in CO2 with no consistent correlation between CO2 level and average global temperature, Fig 10.9.
Figure 10.9: CO2
and average global temperature over geologic time (time scale is logarithmic).
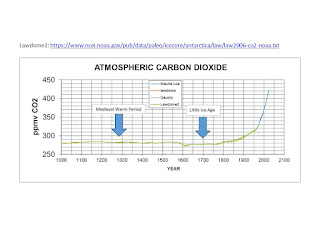
The atmospheric CO2 level has been measured in ice cores extracted at Lawdome Antarctica [41]. Figure 11 shows the CO2 level at Lawdome since the year 1000. This shows that there was negligible CO2 change in spite of the temperature fluctuation from the high of the MWP to the low of the LIA. Perhaps more pointedly, the planet experienced both the MWP and the LIA at very nearly the same CO2 level of 280 ppmv.
Figure 11: Climate
change from MWP high temperature thru LIA low temperature had little effect on
CO2 level,
In Figure 12,
the temperature and CO2 chart constructed from proxy data for the
last 800,000 years and put together by NOAA, clearly shows several periods when
temperature changes preceded CO2 changes. During this period of
comparatively low CO2 level, the atmospheric CO2 level appears to
have been determined by solubility of CO2 in water.
The chart to the right on Figure 12 is to the same vertical scale but expanded in time to show measured data since 1850. This shows a CO2 increase of about 160 ppmv and rising, while temperature, although rising slightly, remains in the range of previous interglacials. The temperature increase of about 1.2 C can be mostly explained by the increase in WV [19] and decrease in cloud cover.
Figure 12: Current
CO2 and temperature to paleo scales.
12. Summary
Section 17 of the analysis at [19] shows that about 2/3 of the average
global temperature increase since 1909 can be attributed to the increase in
Total Precipitable Water (TPW) (AKA Total Column Water). The increase in TPW is
accurately measured by NASA/RSS using satellite-based instrumentation. They
document TPW anomalies monthly in annual reports available on line. The latest
report is available at [5]. The measured rate of increase trend of TPW through
Dec 2024 is 0.0447 kg/m^2/year which is the slope of the regression line in
Figure 5.
From Table 1 the amount of WV put into the atmosphere by
human activity is about 0.92 mm/yr. Average annual rainfall is about a meter
(1000 mm) so human activity only adds about 0.92/1000 = 0.00092 or about 0.09%
to rainfall. Human activity is not contributing significantly to precipitation
increase so the increased TPW must be due mostly to increase in WV average residence
time.
Expected AGT increase assessment is by UAH v6.1. The WV increase from
feedback that UAH temperatures would produce is shown at Figure 7.2. Average residence
times calculated at the end of several different years are shown in Figure 7.1.
The total increase in average residence time in 36 years is about 13*36 = 468 minutes
= 7.8 hr.
From Table 1 in Section 19 of [19] the total contribution to AGT increase 1895
thru 2023 from WV increase is about 0.9 K.
Conclusion
Humanity’s direct contribution to precipitation and therefore WV increase is shown to be
small so increased atmospheric water vapor is essentially all from
increased AGT and increased average residence time of the WV in the atmosphere. Increased
CO2 has negligible effect on warming. Climate Sensitivity, the
temperature increase from doubling CO2, is not significantly
different from zero.
26. Ice and mixed phase clouds: http://www.cas.manchester.ac.uk/resactivities/cloudphysics/background/ice/
27. Wexler, vapor pressure of
water: https://www.ncbi.nlm.nih.gov/pmc/articles/PMC5312760/
28. Wexler, thermodynamic
calculations for the vapor pressure of ice: https://nvlpubs.nist.gov/nistpubs/jres/81A/jresv81An1p5_A1b.pdf
30. HadCRUT4 data: http://www.metoffice.gov.uk/hadobs/hadcrut4/data/current/time_series/HadCRUT.4.6.0.0.monthly_ns_avg.txt
31. HadCRUT5 data: https://www.metoffice.gov.uk/hadobs/hadcrut5/data/current/download.html
32. Theory of Redirected energy: https://energyredirect3.blogspot.com
33. Water vapor generated by humanity has been 90% from irrigation: https://agupubs.onlinelibrary.wiley.com/doi/full/10.1029/2001WR000355
34. Ground level WV 5 g/kg ≈ 8000
ppmv in 1992: https://www.eso.org/gen-fac/pubs/astclim/espas/pwv/mockler.html Fig 1
35. Ground level WV 8,000 ppm WV
vs altitude Spectralcalc: https://www.spectralcalc.com/atmosphere_browser/modify_atmosphere.php
36. Water use: https://www.fao.org/aquastat/en/overview/methodology/water-use
37. Pearson coefficient
calculator: https://www.socscistatistics.com/tests/pearson/default2.aspx
38. p-value calculator: https://www.danielsoper.com/Statcalc/calculator.aspx?id=44
39. Ave global WV: https://www.labxchange.org/library/items/lb:LabXchange:328c385b:html:1
40. Wallace and Hobbs: http://www.gnss-x.ac.cn/docs/Atmospheric%20Science%20An%20Introductory%20Survey%20(John%20M.%20Wallace,%20Peter%20V.%20Hobbs)%20(z-lib.org).pdf
41. Ice core measurements of CO2 at Lawdome Antarctica: https://www.ncei.noaa.gov/pub/data/paleo/icecore/antarctica/law/law2006-co2-noaa.txt42. UAH 6.1 temperatures: https://www.nsstc.uah.edu/data/msu/v6.1/tlt/uahncdc_lt_6.1.txt
43. SST anomalies from Climatereanalyzer: https://climatereanalyzer.org/clim/sst_monthly/?dm_id=world_60s-60n&var_id=sstanom
44. SST anomalies from EPA: https://www.epa.gov/climate-indicators/climate-change-indicators-sea-surface-temperature
45. SST anomalies from NOAA (wayback
machine): http://www.ncdc.noaa.gov/sotc/global/201509
46 SST anomalies from Hadset4: https://www.metoffice.gov.uk/hadobs/hadsst4/data/download.html





















Very interesting paper and thanks for sharing it Dan.
ReplyDeleteWho is the author?
DeleteDan Pangburn, P.E. (ret), MSME, ASME life member
DeleteAgree, very important investigation.
ReplyDeleteThe key is to simplify.
We know the black body temperature steady state temperature of the earth which can easilly be calculated to -18 Celsius, meaning without atmosphere.
We know aveage earth temperature today which is + 14 C Celcius.
I am trying to corelate the two and need discussion about CO2 and WV H2O. Most important how many Watt -1 Tonn of each backscatter..
Without the Atmosphere as we know today, the black body steady state temperature of the earth would be different from -18 C due to Oceans.
ReplyDeleteThe -18 C assumes albedo of 0.3 which would not hold if no atmosphere. Also, if no atmosphere there would be no water vapor and no oceans.
DeleteSo what do we do about the irrigation problem?
ReplyDeleteWater vapor, and warming from increased WV, is limited by how much WV the atmosphere will hold. The amount of warming possible from increased WV appears to be less than a degree K and not a problem. Global cooling, portended by the quiet sun, is a far greater threat. The warming from increased WV is countering that, will slow and possibly prevent it
DeleteThis comment has been removed by the author.
DeleteGreat article (I'm a retired CEng). Nice statement re WV warming balancing quietening sun! Trying to convince youngsters they're not about to die through CO2 climate change is a challenge.
ReplyDeleteThanks. It seems a higher % of engineers figure it out than others.
ReplyDeleteChemical Engineer by training, now missionary to Haiti. In college Univ of Texas at Austin, one of my classes was a heat and material balance of the earth. It stretched my mind.
Deleteyes the engineer/scientist divide is often amusingly stark
Deletei like to joke that a scientist's job is to come up with a thousand ideas in hopes that one might move us a little closer to the truth, whereas an engineers' job is avoid a thousand fatal mistakes in one real-world application so that it works every time
In researching scientific data on climate after retirement from spending 40 years researching and designing jet engines, I discovered that the water vapor component of the atmosphere is about 75 times that of CO2 and became very suspicious of the IPCC claims about CO2. I am fascinated with this in -depth analysis, which shows the dominance of water vapor. Very gratifying!
ReplyDeleteHi Dan, I found your paper very interesting... do you have a rough idea how the total WV content of the atmosphere compare to human WV emissions?
ReplyDeletewondered a few years back how much human water usage would have to increase to affect sea levels and after some BOE calcs the answer there seems to be “by a few orders of magnitude” but then of course the hydrosphere masses about 300x what the atmosphere does so that seems like it might be in a relevant ballpark for WV
at any rate the idea human WV emissions might directly affect temp and thus CO2 levels is certainly intriguing... might help explain several discrepancies in the IPCC view... hope you are able to write more
Not much. In Section 6 it is calculated that humanity adds on average only about 0.00026% to the average precipitation.
Deletethanks, interesting
DeleteOops, I discovered a factor of 1000 error (Its been fixed). Humanity adds on average only about 0.26% to the average precipitation.
DeleteVery interesting. One large-scale climate effect of irrigation I know myself---for the past 30 years, the North India plains (including West Punjab and East Bengal) have seen far more winter fogs than were known previously. This coincides with a great increase in tube-well irrigation and consequent groundwater extraction on a massive scale.
ReplyDeleteI think that only the ground water extraction component of the irrigation should be included in your estimate of 3986 km3 of total irrigation. The surface water is merely being shifted from one place to another. Only the groundwater extraction adds to the surface water quantity.
Gyan, My argument for including surface water there is that the area where evaporation takes place is what matters and essentially all of the surface water would be spread out adding to the evaporation area without significantly diminishing the surface area of its source. Realize that this was just a sanity check and did not contribute to the findings shown in Table 1.
DeleteHow does water vapour account for regular abrupt climate changes of Dansgaard-Oeschger events during the glacial cycle?
ReplyDeleteIt doesn't. Human influence on WV was tiny prior to about 1800 and the rate increased dramatically around 1960.
DeleteDan, most interesting. However, I don't understand where you've gotten your extrapolation of water vapor back to the year 1600 ... what did I miss?
ReplyDeleteMy best to you,
w.
W,
DeleteYou didn't miss anything. I had developed the extrapolation in 2016 for use in http://globalclimatedrivers2.blogspot.com. The graph appears as Fig 3 there with very brief explanation (and wrong coefficient, I actually use 4.5247, not 4.5118). I used smoothed CO2 as a proxy and the resultant graph looks reasonable to me. I found these notes where I did it:
TPW = X (CO2 ppmv)^Y
𝑌= (ln(𝑇𝑃𝑊1−ln(𝑇𝑃𝑊2)/(ln(𝐶𝑂2,1)−ln(𝐶𝑂2,2))
X = TPW1/CO2,1^Y
1. Linear eqn thru TPW data
2. Calc TPW1 & TPW2 from [linear regression] eqn
3. Select CO2,1 & CO2,2 frm [smothed] data [for same time interval?]
[That second equation should be: 𝑌= (ln(𝑇𝑃𝑊1)−ln(𝑇𝑃𝑊2))/(ln(𝐶𝑂2,1)−ln(𝐶𝑂2,2))
Thanks for the clarification, Dan. What I'm still not understanding is why you think that TPW varies linearly with the log of CO2 ... where is the observational evidence for that relationship?
Deletew.
The temperature varies with the log of CO2 or also with the log of WV (your work). Things proportional to the same thing are proportional to each other.
DeleteThanks so much for this illuminating analysis, Dan. Has anything like this been published in a peer-reviewed journal? I am not aware of anything that targets increased irrigation. You make a good case for the role of increased irrigation in the increase in global temperature in recent decades.
ReplyDeleteSee:
Deletehttps://digitalcommons.unl.edu/cgi/viewcontent.cgi?article=1195&context=natrespapers
w.
Thanks for the comments. IMO the key discovery is that water vapor has been increasing faster than possible from just planet warming (feedback) (Sect 7). This refutes the popular theory that CO2 with feedback caused the warming. The survey to find the source of the 'extra' water vapor was just out of curiosity. Later I found out that it corroborated an earlier study published by AGU. It is listed as Ref 33.
DeleteThanks for your response, Dan. Yes, I noted your strong point about the water vapor increasing faster than just planet warming would explain. I have not seen any other work that identifies the increase in global irrigation as a significant factor in recent global warming, but it makes sense. It would be nice to see your work get broader exposure through being published in a journal. Thanks again. Don
Delete@ Willis: thanks for the reference. I found several of these sorts of studies, but they are looking at local/regional effects, not global. It does raise the issue of advancing irrigation into semi-desert areas causing a decreased albedo, which of itself could cause warming, aside from the effect of raised humidity.
DeleteDan, I saw your comment on twitter and returned to discuss this further with some new data.
ReplyDeleteWe have reasonable gridded SST (Reynolds OI) and TPW (RSS) data from Jan 1988 to Jan 2023.
Using those, I calculate that the average global change in TPW per 1°C rise in SST is 1.9 kg/m2 per °C. This is well below your estimate.
https://rosebyanyothernameblog.wordpress.com/wp-content/uploads/2024/10/global-tpw-vs-sst-trend.png
However, that is FAR from a linear function. Up to a SST of about 18°C, it's pretty steady at ~ 0.6 kg/m2 per °C. At that point it starts to rise faster and faster, reaching a max increase of ~6 kg/m2 per °C in the hottest tropics.
https://rosebyanyothernameblog.wordpress.com/wp-content/uploads/2024/10/scatter-tpw-vs-temp.png
Sadly, because of both the difference in the average from yours and the wild non-linearity of the TPW trend vs SST, I fear your calculations are not valid.
My best to you and yours,
w.
W, thank you for your comments. It appears that your assessment corroborates my admittedly somewhat crude determination of the effect of temperature change on TPW change. Average 1.9 kg/m^2/C is about average 6.7%/C which is what I used (see Sect 7).
DeleteThanks, Dan. You are correct that the 1.9 kg/m2 per °C is about the percentage you list. My bad, I hadn't noticed the units.
DeleteHowever, the problem of the extreme non-linearity of the relationship between TPW and temperature remains …
Regards,
w.
W, IMO the profile of the non-linearity hasn't changed enough to change the conclusions.
DeleteDan your original blackbody theoretical curve is for 47 C or 320 K NOT 21 C or 294 K as shown
ReplyDeleteThe 294 is NASA's number. I never checked it but it looks consistent with the BB curves on Fig 1.5 from U Chicago.
Delete